AI-in-the-loop Workflow

This is an example of how Dragon can be used to execute an AI-in-the-loop workflow. Inspiration for this demo comes from the NERSC-10 Workflow Archetypes White Paper. This workflow most closely resembles the workflow scenario given as part of archetype four.

In this example we use a small model implemented in PyTorch to compute an approximation to \(\sin(x)\). In parallel to doing the inference with the model, we launch sim-cheap on four MPI ranks. This MPI job computes the Taylor approximation to \(\sin(x)\) and compares this with the output of the model. If the difference is less than 0.05 we consider the model’s approximation to be sufficiently accurate and print out the result with the exact result. If the difference is larger than 0.05 we consider this a failure and re-train the model on a new set of data.

To generate this data we launch sim-expensive. This MPI job is launched on eight ranks-per-node and each rank generates 32 data points of the form \((x, \sin(x))\) where \(x \in U(-\pi, \pi)\). This data is aggregated into a PyTorch tensor and then used to train the model. We then re-evaluate the re-trained model and decide if we need to re-train again or if the estimate is sufficiently accurate. We continue this loop until we’ve had five successes.

Fig. 7 presents the structure of this main loop. It shows when each MPI application is launched and what portions are executed in parallel.

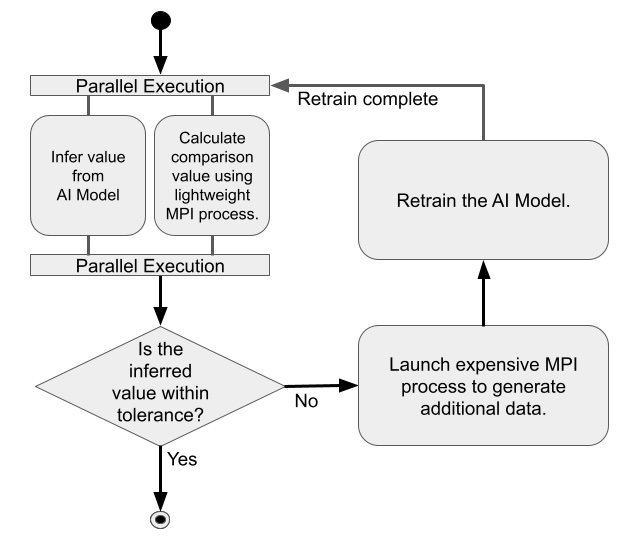
../_images/ai-in-the-loop-workflow.jpg

Fig. 7 Example AI-in-the-loop workflow

This example consists of the following python files:

  • ai-in-the-loop.py - This is the main file. It contains functions for launching both MPI executables and parsing the results as well as imports functions defined in model.py and coordinates the model inference and training with the MPI jobs.

  • model.py - This file defines the model and provides some functions for model training and inference.

Below, we present the main python code (ai-in-the-loop.py) which acts as the coordinator of the workflow. The code of the other files can be found in the release package, inside examples/workflows/ai-in-the-loop directory.

Listing 11 ai-in-the-loop.py: Main orchestrator for AI-in-the-loop demo
  1import dragon
  2import multiprocessing as mp
  3
  4import os
  5import math
  6import torch
  7from itertools import count
  8from model import Net, make_features, infer, train
  9
 10from dragon.native.process import Process, ProcessTemplate, Popen
 11from dragon.native.process_group import ProcessGroup
 12from dragon.infrastructure.connection import Connection
 13from dragon.native.machine import System
 14
 15
 16def parse_results(stdout_conn: Connection) -> tuple:
 17    """Read stdout from the Dragon connection.
 18
 19    :param stdout_conn: Dragon connection to rank 0's stdout
 20    :type stdout_conn: Connection
 21    :return: tuple with a list of x values and the corresponding sin(x) values.
 22    :rtype: tuple
 23    """
 24    x = []
 25    y = []
 26    output = ""
 27    try:
 28        # this is brute force
 29        while True:
 30            output += stdout_conn.recv()
 31    except EOFError:
 32        pass
 33    finally:
 34        stdout_conn.close()
 35
 36    split_line = output.split("\n")
 37    for line in split_line[:-1]:
 38        try:
 39            x_val = float(line.split(",")[0])
 40            y_val = float(line.split(",")[1])
 41            x.append(x_val)
 42            y.append(y_val)
 43        except (IndexError, ValueError):
 44            pass
 45
 46    return x, y
 47
 48
 49def generate_data(
 50    num_ranks: int, samples_per_rank: int, sample_range: list, number_of_times_trained: int
 51) -> tuple:
 52    """Launches mpi application that generates (x, sin(x)) pairs uniformly sampled from [sample_range[0], sample_range[1]).
 53
 54    :param num_ranks: number of ranks to use to generate data
 55    :type num_ranks: int
 56    :param samples_per_rank: number of samples to generate per rank
 57    :type samples_per_rank: int
 58    :param sample_range: range from which to sample training data
 59    :type sample_range: list
 60    :param number_of_times_trained: number of times trained. can be used to set a seed for the mpi application.
 61    :type number_of_times_trained: int
 62    :return: tuple of PyTorch tensors containing data and targets respectively
 63    :rtype: tuple
 64    """
 65    """Launch process group and parse data"""
 66    exe = os.path.join(os.getcwd(), "sim-expensive")
 67    args = [str(samples_per_rank), str(sample_range[0]), str(sample_range[1]), str(number_of_times_trained)]
 68    run_dir = os.getcwd()
 69
 70    grp = ProcessGroup(restart=False, pmi_enabled=True)
 71
 72    # Pipe the stdout output from the head process to a Dragon connection
 73    grp.add_process(nproc=1, template=ProcessTemplate(target=exe, args=args, cwd=run_dir, stdout=Popen.PIPE))
 74
 75    # All other ranks should have their output go to DEVNULL
 76    grp.add_process(
 77        nproc=num_ranks - 1,
 78        template=ProcessTemplate(target=exe, args=args, cwd=run_dir, stdout=Popen.DEVNULL),
 79    )
 80    # start the process group
 81    grp.init()
 82    grp.start()
 83    group_procs = [Process(None, ident=puid) for puid in grp.puids]
 84    for proc in group_procs:
 85        if proc.stdout_conn:
 86            # get info printed to stdout from rank 0
 87            x, y = parse_results(proc.stdout_conn)
 88    # wait for workers to finish and shutdown process group
 89    grp.join()
 90    grp.stop()
 91    # transform data into tensors for training
 92    data = torch.tensor(x)
 93    target = torch.tensor(y)
 94    return data, target.unsqueeze(1)
 95
 96
 97def compute_cheap_approx(num_ranks: int, x: float) -> float:
 98    """Launch process group with cheap approximation and parse output to float as a string
 99
100    :param num_ranks: number of mpi ranks (and therefor terms) to use for the cheap approximation
101    :type num_ranks: int
102    :param x: point where you are trying to compute sin(x)
103    :type x: float
104    :return: Taylor expansion of sin(x)
105    :rtype: float
106    """
107    exe = os.path.join(os.getcwd(), "sim-cheap")
108    args = [str(x)]
109    run_dir = os.getcwd()
110
111    grp = ProcessGroup(restart=False, pmi_enabled=True)
112
113    # Pipe the stdout output from the head process to a Dragon connection
114    grp.add_process(nproc=1, template=ProcessTemplate(target=exe, args=args, cwd=run_dir, stdout=Popen.PIPE))
115
116    # All other ranks should have their output go to DEVNULL
117    grp.add_process(
118        nproc=num_ranks - 1,
119        template=ProcessTemplate(target=exe, args=args, cwd=run_dir, stdout=Popen.DEVNULL),
120    )
121    # start the process group
122    grp.init()
123    grp.start()
124    group_procs = [Process(None, ident=puid) for puid in grp.puids]
125    for proc in group_procs:
126        # get info printed to stdout from rank 0
127        if proc.stdout_conn:
128            _, y = parse_results(proc.stdout_conn)
129    # wait for workers to finish and shutdown process group
130    grp.join()
131    grp.stop()
132
133    return y
134
135
136def infer_and_compare(model: torch.nn, x: float) -> tuple:
137    """Launch inference and cheap approximation and check the difference between them
138
139    :param model: PyTorch model that approximates sin(x)
140    :type model: torch.nn
141    :param x: value where we want to evaluate sin(x)
142    :type x: float
143    :return: the model's output val and the difference between it and the cheap approximation value
144    :rtype: tuple
145    """
146    with torch.no_grad():
147        # queues to send data to and from inference process
148        q_in = mp.Queue()
149        q_out = mp.Queue()
150        q_in.put((model, x))
151        inf_proc = mp.Process(target=infer, args=(q_in, q_out))
152        inf_proc.start()
153        # launch mpi application to compute cheap approximation
154        te_fx = compute_cheap_approx(4, x.numpy()[0])
155        inf_proc.join()
156        model_val = q_out.get()
157        # compare cheap approximation and model value
158        diff = abs(model_val.numpy() - te_fx[0])
159
160    return model_val, diff
161
162
163def main():
164
165    ranks_per_node = 8
166    data_interval = [-math.pi, math.pi]
167    samples_per_rank = 32
168    my_alloc = System()
169    # Define model
170    model = Net()
171    # Define optimizer
172    optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
173    # Load pretrained model
174    PATH = "model_pretrained_poly.pt"
175    checkpoint = torch.load(PATH)
176    model.load_state_dict(checkpoint["model_state_dict"])
177    optimizer.load_state_dict(checkpoint["optimizer_state_dict"])
178
179    number_of_times_trained = 0
180    successes = 0
181
182    generate_new_x = True
183
184    while successes < 5:
185
186        if generate_new_x:
187            # uniformly sample from [-pi, pi)
188            x = torch.rand(1) * (2 * math.pi) - math.pi
189
190        model_val, diff = infer_and_compare(model, x)
191        if diff > 0.05:
192            print(f"training", flush=True)
193            # want to train and then retry same value
194            generate_new_x = False
195            number_of_times_trained += 1
196            # interval we uniformly sample training data from
197            # launch mpi job to generate data
198            data, target = generate_data(
199                my_alloc.nnodes * ranks_per_node, samples_per_rank, data_interval, number_of_times_trained
200            )
201            # train model
202            loss = train(model, optimizer, data, target)
203        else:
204            successes += 1
205            generate_new_x = True
206            print(f" approx = {model_val}, exact = {math.sin(x)}", flush=True)
207
208
209if __name__ == "__main__":
210    mp.set_start_method("dragon")
211    main()

Installation

After installing dragon, the only other dependency is on PyTorch. The PyTorch version and corresponding pip command can be found here (https://pytorch.org/get-started/locally/ ).

` > pip install torch torchvision torchaudio `

Description of the system used

For this example, HPE Cray Hotlum nodes were used. Each node has AMD EPYC 7763 64-core CPUs.

How to run

Example Output when run on 16 nodes with 8 MPI ranks-per-node used to generate data and four MPI ranks to compute the cheap approximation

 1> make
 2gcc -g  -pedantic -Wall -I /opt/cray/pe/mpich/8.1.26/ofi/gnu/9.1/include -L /opt/cray/pe/mpich/8.1.26/ofi/gnu/9.1/lib   -c -o sim-cheap.o sim-cheap.c
 3gcc -g  -pedantic -Wall -I /opt/cray/pe/mpich/8.1.26/ofi/gnu/9.1/include -L /opt/cray/pe/mpich/8.1.26/ofi/gnu/9.1/lib  sim-cheap.o -o sim-cheap -lm -L /opt/cray/pe/mpich/8.1.26/ofi/gnu/9.1/lib -lmpich
 4gcc -g  -pedantic -Wall -I /opt/cray/pe/mpich/8.1.26/ofi/gnu/9.1/include -L /opt/cray/pe/mpich/8.1.26/ofi/gnu/9.1/lib   -c -o sim-expensive.o
 5gcc -g  -pedantic -Wall -I /opt/cray/pe/mpich/8.1.26/ofi/gnu/9.1/include -L /opt/cray/pe/mpich/8.1.26/ofi/gnu/9.1/lib  sim-expensive.o -o sim-expensive -lm -L /opt/cray/pe/mpich/8.1.26/ofi/gnu/9.1/lib -lmpich
 6> salloc --nodes=16 --exclusive
 7> dragon ai-in-the-loop.py
 8training
 9approx = 0.1283823400735855, exact = 0.15357911534767393
10training
11approx = -0.41591891646385193, exact = -0.4533079140996079
12approx = -0.9724616408348083, exact = -0.9808886564963794
13approx = -0.38959139585494995, exact = -0.4315753703483373
14approx = 0.8678910732269287, exact = 0.8812041533601648